Julius Kesten

zu vergeben

Motivation

Bei der Auslegung elektrischer Maschinen ist der Wirkungsgrad ein zentrales Optimierungsziel. So ermöglichen hohe Wirkungsgrade im Kontext batterieelektrischer Traktion beispielsweise größere Reichweiten. Zur Bestimmung des Wirkungsgrades ist die Kenntnis der in der Maschine auftretenden Verluste relevant.

Ein zentrales Werkzeug bei der Maschinenauslegung stellt die elektromagnetische FEM dar, mittels derer die relevanten Größen numerisch mit ausreichend hoher Genauigkeit bestimmt werden können. Dabei wird die Geometrie der elektrischen Maschine in drei- bzw. viereckige finite Elemente diskretisiert, deren Summe als Mesh (Netz) bezeichnet wird (siehe Abb. 1). Für jedes dieser Elemente wird während der Berechnung das magnetische Vektorpotential bestimmt. Aus diesem Vektorpotential können anschließend die Flussdichten und Feldstärken in der Maschine berechnet und so beispielsweise die Eisenverluste bestimmt werden. Einen wichtigen Bestandteil der Maschinenverluste stellen dabei auch die Verluste in Permanentmagneten dar. Sie sind nicht nur für den Wirkungsgrad relevant, sondern haben auch Einfluss auf die thermischen Grenzen der Maschine.

Aufgabenstellung

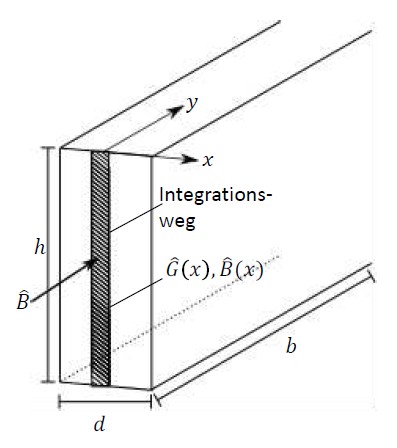
In der Arbeit soll eine Berechnung für Magnetverluste mit dem vorliegenden FEM-Mesh und den zugehörigen Vektorpotentialen realisiert werden. Die Möglichkeit, das Mesh auszuwerten ist dabei gegeben. Mit der entwickelten Lösung sollen sowohl die Wirbelstromverluste (siehe Abb. 2) als auch eventuell auftretende Hystereseverluste in den Magneten bestimmt werden können.

Der Ablauf der Arbeit sieht zunächst eine Recherche zu den Grundlagen der in Permanentmagneten auftretenden Verlustmechanismen in elektrischen Maschinen vor. Anschließend erfolgt die Implementierung der zugrunde liegenden analytischen Zusammenhänge in Matlab. Die programmierten Berechnungen werden in die Auslegungstoolkette des ETI integriert und abschließend mit der beispielhaften Auslegung einer elektrischen Maschine validiert.